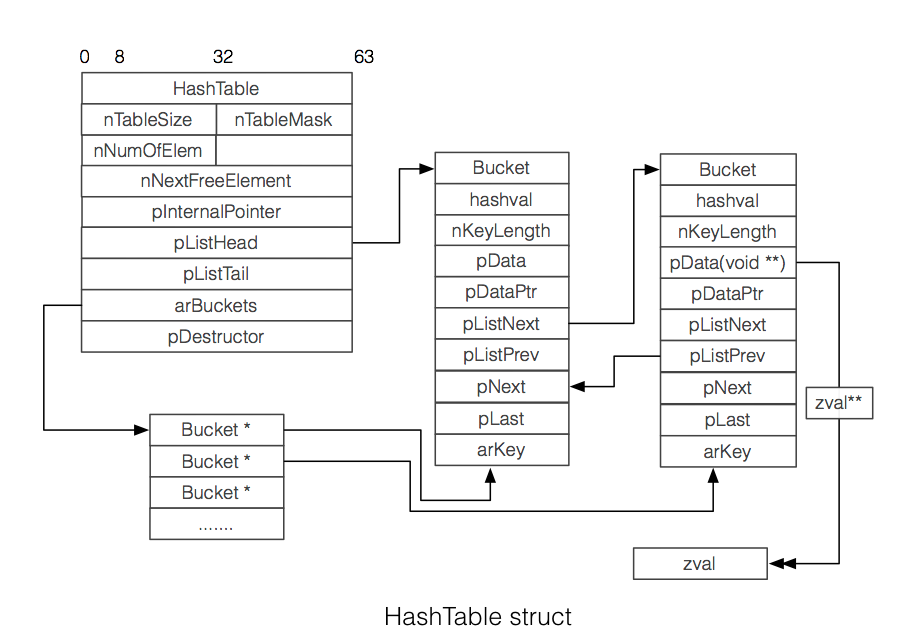
存储容量预估系统设计最重要的项之一。精准的容量预估,可以帮助我们选择最合适存储软件。
本文主要来介绍下Redis几种常用的数据结构,以及内存占用大小。
字符串(SDS)
1 | //SDS的定义如下(sds.h/sdshdr): |
字符串长度不能超过512MB。
下图展示了一个SDS实例:

SDS实例中存储了字符串“Redis”, 该实例中free的值为5(表示未使用的字节为5),len的值为5(表示已使用的字节为5),加上字符数组末尾的”\0”,所以SDS实例占用的总字节数为:(sizeof(int) * 2) + (5 + 5 + 1) = 19,即(len+free)+buf
举例说明
当key长度为 13,value长度为15,key个数为2000,根据上面总结的容量评估模型,容量预估值为 (32 + 16 + 32 + 32) * 2000 + 2048 * 8 = 240384
生产实践
用redis做商品缓存,key为商品id,value为商品信息。key大约占用30个字节,value大约占用1500个字节。
当缓存1百万商品时,容量预估值为(32 + 16 + 64 + 1536) * 1000000+ 1000000(预估) * 8 = 1656000000,约等于1.54G
总结:当value比较大时,占用的内存约等于value的大小*个数
双向链表(List)
1 | //每个链表节点使用一个listNode结构来表示,具体定义如(adlist.h/listNode): |
有序集合(ZSET)
1 | /* ZSETs use a specialized version of Skiplists */ |
zskiplistNode结构占用的总字节数为:24 + 16 * n,n为level数组的大小。
zskiplist结构则用于保存跳跃表节点的相关信息,header和tail分别指向跳跃表的表头和表尾节点,length记录节点总数量,level记录跳跃表中层高最大的那个节点的层数量。zskiplist结构占用的总字节数为32。
字典
1 | typedef struct dictEntry { |
一个Hash存储结构最终会产生以下几个消耗内存的结构:
- 1个SDS结构,用作key字符串,占9个字节(free4个字节+len4个字节+字符串末尾”\0”1个字节);
- 1个dictEntry结构,24字节,负责保存当前的哈希对象;
- 1个redisObject结构,16字节,指向当前key下属的dict结构;
- 1个dict结构,88字节,负责保存哈希对象的键值对;
- n个dictEntry结构,24*n字节,负责保存具体的field和value,n等于field个数;
- n个redisObject结构,16*n字节,用作field对象;
- n个redisObject结构,16*n字节,用作value对象;
- n个SDS结构,(field长度+9)*n字节,用作field字符串;
- n个SDS结构,(value长度+9)*n字节,用作value字符串;
因为hash类型内部有两个dict结构,所以最终会有产生两种rehash,一种rehash基准是field个数,另一种rehash基准是key个数,结合jemalloc内存分配规则,hash类型的容量评估模型为:
总内存消耗 = [key_SDS大小 + redisObject大小 + dictEntry大小 + dict大小 +(redisObject大小 * 2 + field_SDS大小 + val_SDS大小 + dictEntry大小) * field个数 + field_bucket个数 * 指针大小] * key个数 + key_bucket个数 * 指针大小
【换算】
总内存消耗 = [ key_SDS大小 + 16 + 24 + 88 + (16 * 2 + field_SDS大小 + val_SDS大小 + 24) * field个数 + field_bucket个数 * 8] * key个数 + key_bucket个数 * 8
总内存消耗 =[128+ key_SDS大小 +(56 + field_SDS大小 + val_SDS大小 ) * field个数 + field_bucket个数 * 8] * key个数 + key_bucket个数 * 8
集合(SET)
SET的实现其实就是value为null的hash表